# A tibble: 344 × 8
species island bill_len bill_dep flipper_len body_mass sex year
<fct> <fct> <dbl> <dbl> <int> <int> <fct> <int>
1 Adelie Torgersen 39.1 18.7 181 3750 male 2007
2 Adelie Torgersen 39.5 17.4 186 3800 female 2007
3 Adelie Torgersen 40.3 18 195 3250 female 2007
4 Adelie Torgersen NA NA NA NA <NA> 2007
5 Adelie Torgersen 36.7 19.3 193 3450 female 2007
# ℹ 339 more rowsElements of Data Science
SDS 322E
Department of Statistics and Data Sciences
The University of Texas at Austin
Fall 2025
Learning objectives
Understand what problem dimension reduction methods are solving
Apply Principal component analysis to the data
- preprocessing
- compute pca with
prcomp() - extract the first x PCs:
broom::augment() - observe the screen plot to find the optimal number of PCs
- plot the data projected onto the first two PCs
Motivation - dimension reduction
- Hand shadow puppet: 3D hand poses reduced to 2D shadows (Projection)

We want the projection to resemble the original data as much as possible.
Principal component analysis
- Principal component analysis is a linear dimension reduction technique that finds a low-dimensional representation of a dataset that contains as much as possible of the variation.
It can be formulated as an optimization problem to maximize the variance of the projected data, subject to some constraint.
The solution to the optimization happens to be the singular value decomposition of the data matrix \(X\) (if the data has column mean of zero).
All of these will be taken care of by the function
prcomp().
PCA example - Penguins data again
Would you think missing values would be a problem for PCA?
species island bill_len bill_dep flipper_len body_mass sex year
1 Adelie Torgersen 39.1 18.7 181 3750 male 2007
2 Adelie Torgersen 39.5 17.4 186 3800 female 2007
3 Adelie Torgersen 40.3 18.0 195 3250 female 2007
5 Adelie Torgersen 36.7 19.3 193 3450 female 2007
6 Adelie Torgersen 39.3 20.6 190 3650 male 2007
7 Adelie Torgersen 38.9 17.8 181 3625 female 2007PCA example - Penguins data
The function prcomp() in R can be used to perform PCA. The data is centered by default (center = TRUE).
- We would also like to scale the data (
scale = TRUE) since the features are measured in different units (mm vs g). - You may separately center and scale the data before applying PCA and set
center = FALSEandscale = FALSE.
Standard deviations (1, .., p=4):
[1] 1.6569115 0.8821095 0.6071594 0.3284579
Rotation (n x k) = (4 x 4):
PC1 PC2 PC3 PC4
bill_len 0.4537532 -0.60019490 -0.6424951 0.1451695
bill_dep -0.3990472 -0.79616951 0.4258004 -0.1599044
flipper_len 0.5768250 -0.00578817 0.2360952 -0.7819837
body_mass 0.5496747 -0.07646366 0.5917374 0.5846861Penguins data - Inspect the PCA results
- eigenvalue: standard deviations of the principal components - their square capture the variance explained by each PC
- rotation: principal components (eigenvectors) - directions of maximum variance
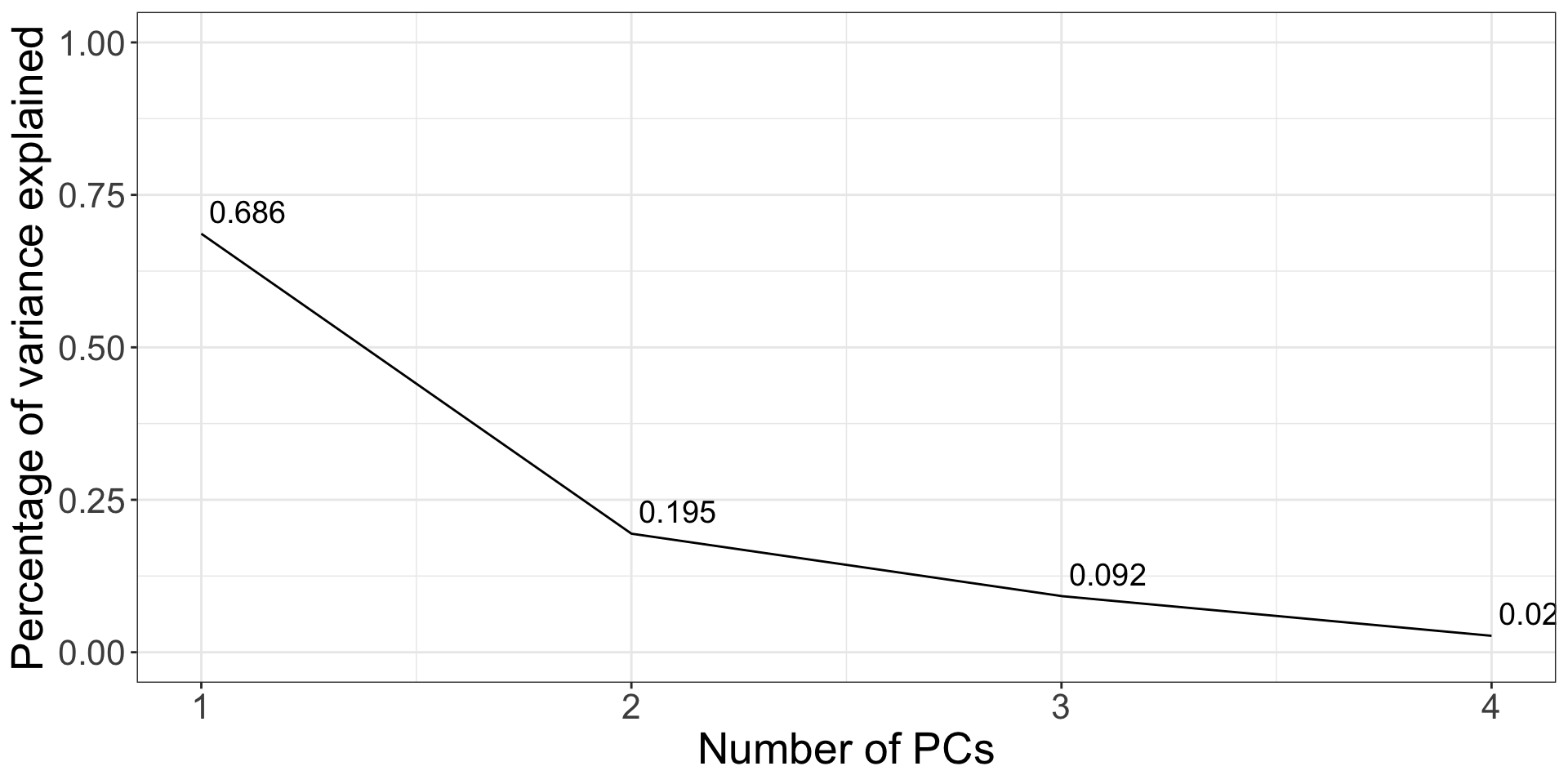
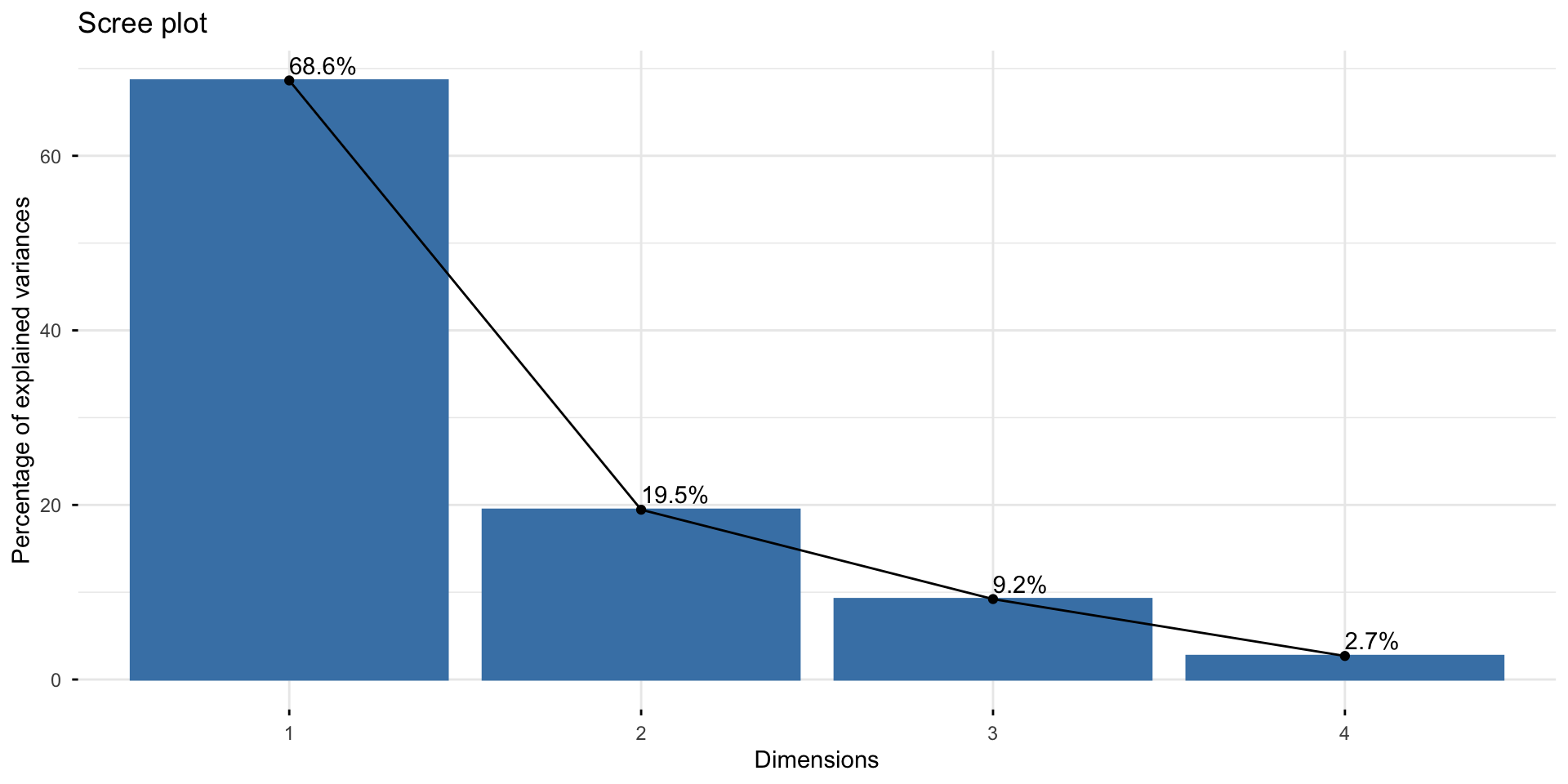
Diagnostics: Choose k
This plot is called a scree plot - used to tell the number of principal components to retain. Choose the number at the “elbow” point: k = 2 here.
Scree plot
The fviz_screeplot() function from the factoextra package allows you to plot the scree plot in one command.
Diagnostics: plot the first 2 PCs
Obtain the projected data:
Option 1: use base R predict()
Option 2: use broom::augment()
# A tibble: 333 × 13
.rownames species island bill_len bill_dep flipper_len body_mass
<chr> <fct> <fct> <dbl> <dbl> <int> <int>
1 1 Adelie Torgersen 39.1 18.7 181 3750
2 2 Adelie Torgersen 39.5 17.4 186 3800
3 3 Adelie Torgersen 40.3 18 195 3250
4 5 Adelie Torgersen 36.7 19.3 193 3450
5 6 Adelie Torgersen 39.3 20.6 190 3650
# ℹ 328 more rows
# ℹ 6 more variables: sex <fct>, year <int>, .fittedPC1 <dbl>,
# .fittedPC2 <dbl>, .fittedPC3 <dbl>, .fittedPC4 <dbl>Diagnostics: plot the first 2 PCs
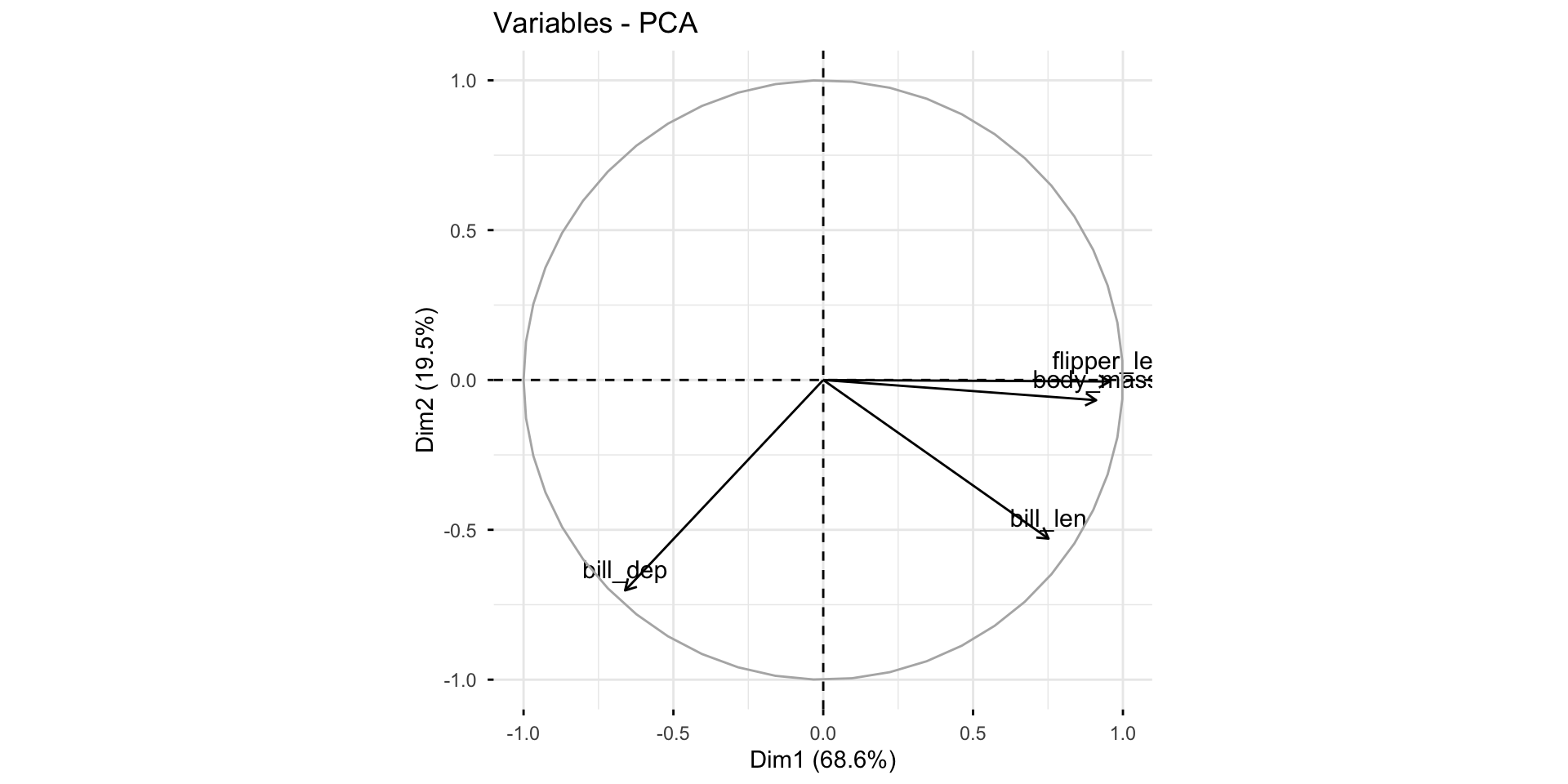
Diagnostics: plot the first 2 PCs
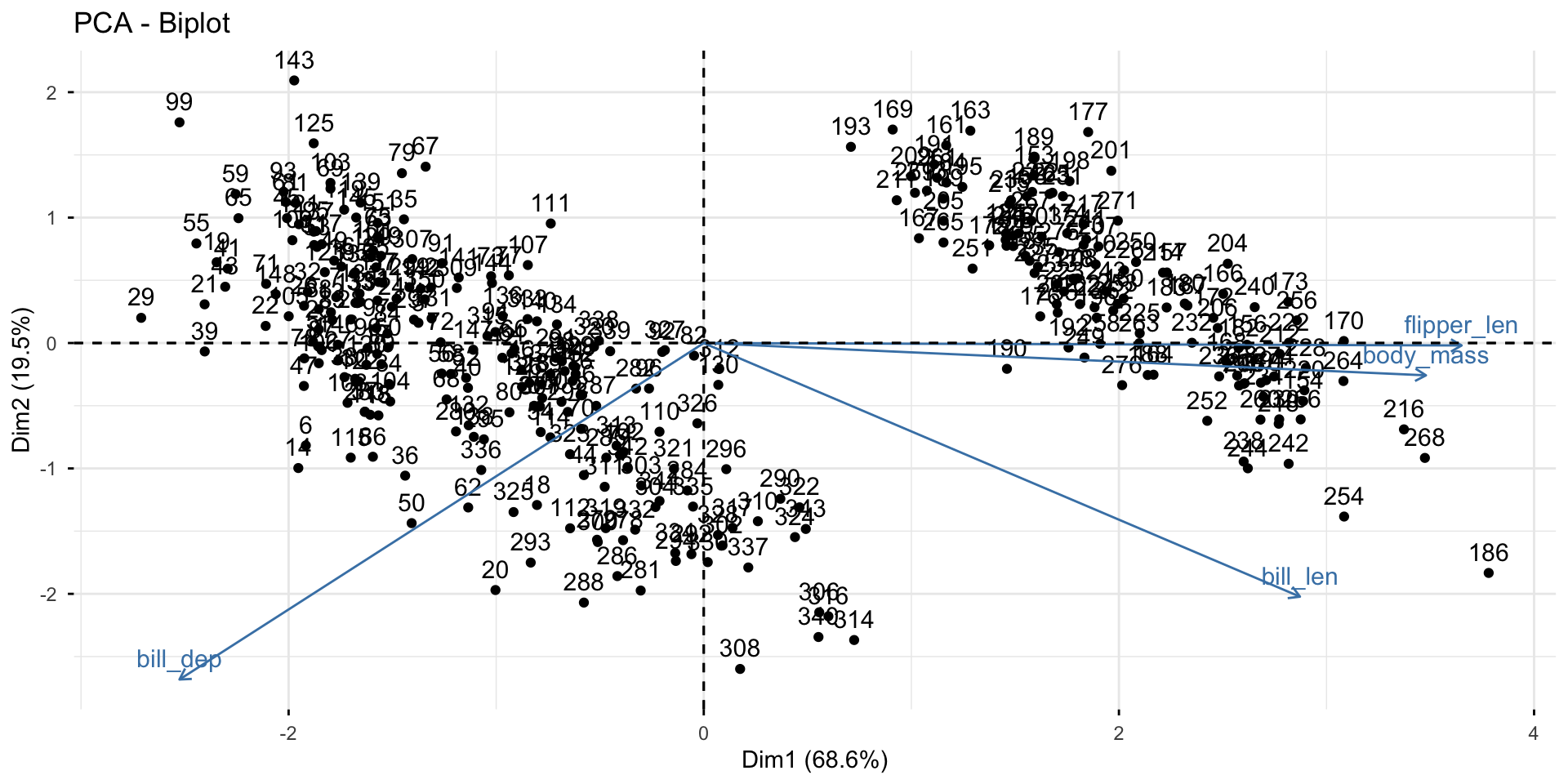
Diagnostics: plot the first 2 PCs
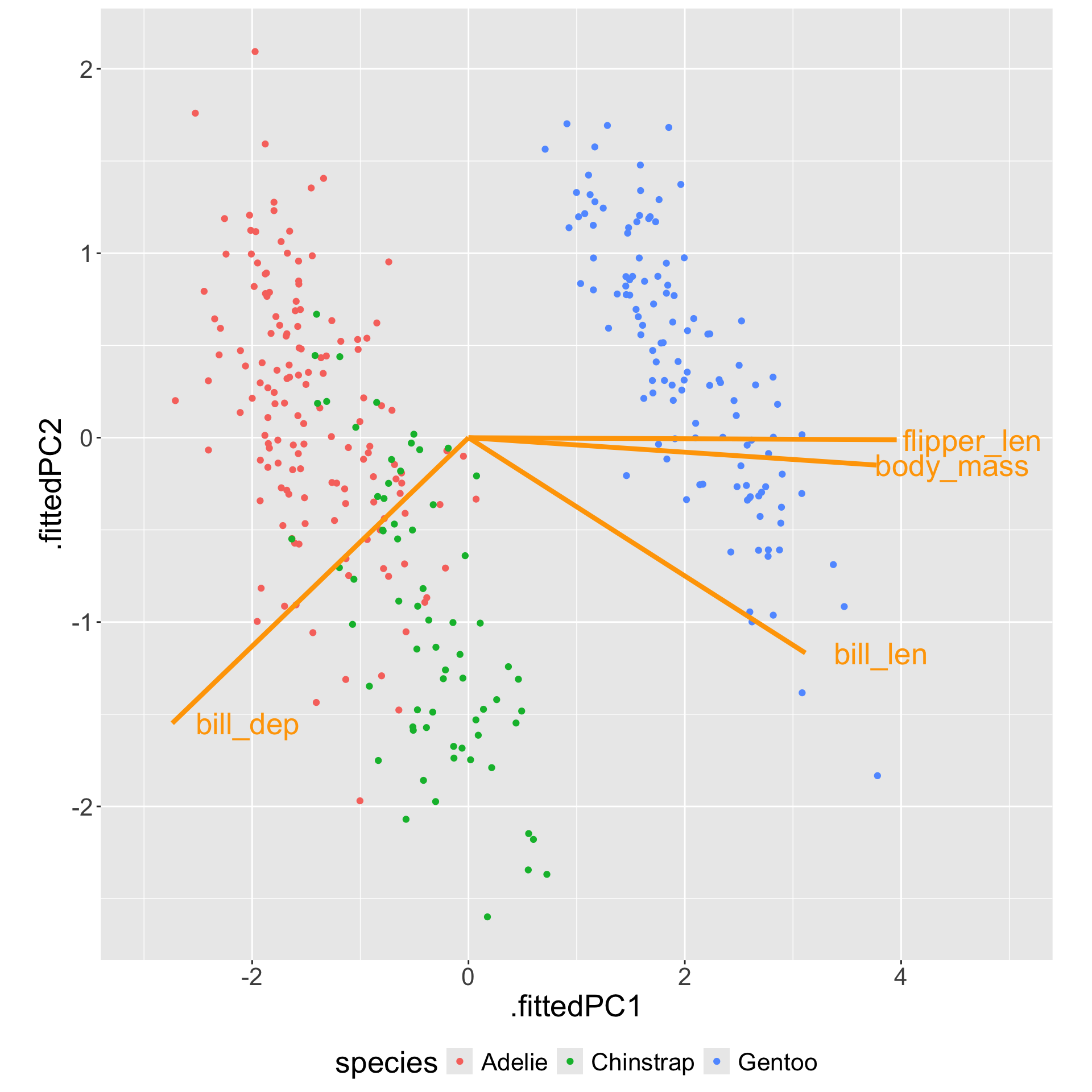
Gentoo can be separated from the other two species by bill depth (PC1).
Among Adelie and Chinstrap, bill length helps separate them (PC2).
This matches with the summary statistics:
# A tibble: 3 × 3
species bill_dep bill_len
<fct> <dbl> <dbl>
1 Adelie 18.3 38.8
2 Chinstrap 18.4 48.8
3 Gentoo 15.0 47.6What’s more
- Principal component analysis (PCA) is a linear dimension reduction method, there are other linear methods, e.g.
- Projection Pursuit (PP)
- There are also non-linear dimension reduction methods, e.g.
- Multidimensional Scaling (MDS),
- T-stochastic Neighbourhood Embedding (t-SNE), and
- Uniform manifold Approximation and Projection (UMAP)
Appendix
Data:
\[\begin{aligned} X_{n\times p} & = [X_{1} \enspace X_{2} \enspace \dots \enspace X_{p}]_{n\times p} \\ & = \left[ \begin{array}{cccc} x_{11} & x_{12} & \dots & x_{1p} \\ x_{21} & x_{22} & \dots & x_{2p}\\ \vdots & \vdots & & \vdots \\ x_{n1} & x_{n2} & \dots & x_{np} \end{array} \right]_{n\times p} \end{aligned}\]We require column means of \(X\) to be zero (centered data): \(\bar{X_i} = 0\)
Principal component analysis
In PCA, \(\Phi\) is called the rotation or the loading matrix:
\[\begin{aligned} \Phi_{p \times k} & = [\phi_{1} \enspace \phi_{2} \enspace \dots \enspace \phi_{k}]_{p\times k} \\ & = \left[ \begin{array}{cccc} \phi_{11} & \phi_{12} & \dots & \phi_{1k} \\ \phi_{21} & \phi_{22} & \dots & \phi_{2k}\\ \vdots & \vdots & & \vdots \\ \phi_{p1} & \phi_{p2} & \dots & \phi _{pk} \end{array} \right]_{p\times k} \end{aligned}\]\(\Phi\) satisfies two conditions:
- It is normalized: \(\sum _{i=1}^{p} \phi_{ij}^2 = 1\) for \(j = 1, \dots, k\) and
- Vectors are orthogonal to each other: \(\sum_{i=1}^{p} \phi_{ij}\phi_{ik} = 0\) for \(j \neq k\).
(We will talk about why this is the case in a second.)
Principal component analysis
Principal components are the linear combinations of the original variables:
The first principal component (PC1):
\[\begin{aligned} Z_1 = \begin{bmatrix} z_{11} \\ z_{21} \\ \vdots \\ z_{n1}\end{bmatrix} &= \phi_{11} \begin{bmatrix} x_{11} \\ x_{21} \\ \vdots \\ x_{n1}\end{bmatrix} + \phi_{21} \begin{bmatrix} x_{12} \\ x_{22} \\ \vdots \\ x_{n2}\end{bmatrix} + \dots + \phi_{p1}\begin{bmatrix} x_{1p} \\ x_{2p} \\ \vdots \\ x_{np}\end{bmatrix} \\ &= \phi_{11}X_1 + \phi_{21}X_2 + \dots + \phi_{p1}X_p \\ \end{aligned}\]where \(\sum _{i=1}^{p} \phi_{i1}^2 = 1\) and \(\bar{Z_i} = 0\) (since \(\bar{X_i} = 0\))
Principal component analysis
For each element in \(Z_1\): \(z_{i1} = \phi_{11}x_{i1} + \phi_{21}x_{i2} + \dots + \phi_{p1}x_{ip} = \sum_{j = 1}^p \phi_{j1} x_{ij}\)
Write down the variance of \(Z_1\):
\[\text{Var}(Z_1) = E(Z_1^2) = \frac{1}{n}\sum_{i = 1}^n z_{i1}^2=\frac{1}{n}\sum_{i = 1}^n (\sum_{j = 1}^p \phi_{j1} x_{ij})^2 \]
We would like to find the direction (the coefficients \(\phi_{j1}\)’s) that maximizes the variance of \(Z_1\):
\[\max_{\phi_{11}, \dots, \phi_{p1}} \text{Var}(Z_1) = \max_{\phi_{11}, \dots, \phi_{p1}} \frac{1}{n}\sum_{i = 1}^n (\sum_{j = 1}^p \phi_{j1} x_{ij})^2 \] subject to the normalization constraint \(\sum _{i=1}^{p} \phi_{i1}^2 = 1\).
Optimization
\[\text{Var}(Z_1) = E(Z_1^2) = \frac{1}{n}\sum_{i = 1}^n z_{i1}^2 = \left\lVert z_{1} \right\rVert^2 = \left\lVert X\phi_1 \right\rVert^2 = \phi_1^T X^T X \phi_1\]
subject to \(\phi_1^T \phi_1 = 1\)
Use Lagrange multipliers to solve the constrained optimization problem:
\[ L(\phi_1, \lambda) = \phi_1^T X^T X \phi_1 - \lambda (\phi_1^T \phi_1 - 1)\] Take the derivative and set it to zero gives \[X^TX\phi_1 = \lambda \phi_1\]
This is the eigenvalue equation for the matrix \(X^TX\).
Recognize \(X^TX\) is related the covariance matrix: \(S = \frac{1}{n-1}X^TX\), the first principal component (\(\phi_1\)) is the eigenvector of \(X^TX\) corresponding to the largest eigenvalue.
Computation
The first principal component (\(\phi_1\)) is the eigenvector of \(X^TX\) corresponding to the largest eigenvalue. This can be obtained through:
- Singular value decomposition (SVD) of \(X\) (always apply):
\[X = UDV^T\]
- Eigen-decomposition of \(X^TX = (n-1) S\) (since \(X^TX\) is square):
\[X^TX = V D^2 V^T\]
where
- \(X\) is a \(n \times p\) matrix
- \(U\) is a \(n \times n\) orthogonal matrix (\(U^TU = 1\))
- \(D\) is a \(n \times p\) diagonal matrix with non-negative elements (square root of the eigenvalues of \(X^TX\) arranged in descending order)
- \(V\) is a \(p \times p\) orthogonal matrix (eigenvectors: \(V^TV = 1\))
Principal component analysis
The second principal component (PC2): \(Z_2 = \phi_{12}X_1 + \phi_{22}X_2 + \dots + \phi_{p2}X_p\)
The second principal component is the linear combination of \(X_1, X_2, \dots, X_p\) that has the largest variance out of all linear combinations that are uncorrelated with \(Z_1\).
subject to “\(Z_2\) being uncorrelated with \(Z_1\)”.
This is equivalent to constraining \(\phi_2\) to be orthogonal to \(\phi_1\), hence
\[\max_{\phi_{12}, \dots, \phi_{p2}} \text{Var}(Z_2) = \max_{\phi_{12}, \dots, \phi_{p2}} \frac{1}{n}\sum_{i = 1}^n (\sum_{j = 1}^p \phi_{j2} x_{ij})^2 \] subject to the normalization constraint \(\sum _{i=1}^{p} \phi_{i2}^2 = 1\) and the orthogonality constraint \(\sum_{i=1}^{p} \phi_{i1}\phi_{i2} = 0\).