Elements of Data Science
SDS 322E

H. Sherry Zhang
Department of Statistics and Data Sciences
The University of Texas at Austin

Fall 2025

Learning objectives

  • Understand the basic idea of decision trees for regression and classification
  • Fit decision trees using tidymodels for both regression and classification tasks
  • Identify the key parameters of decision trees and their effects

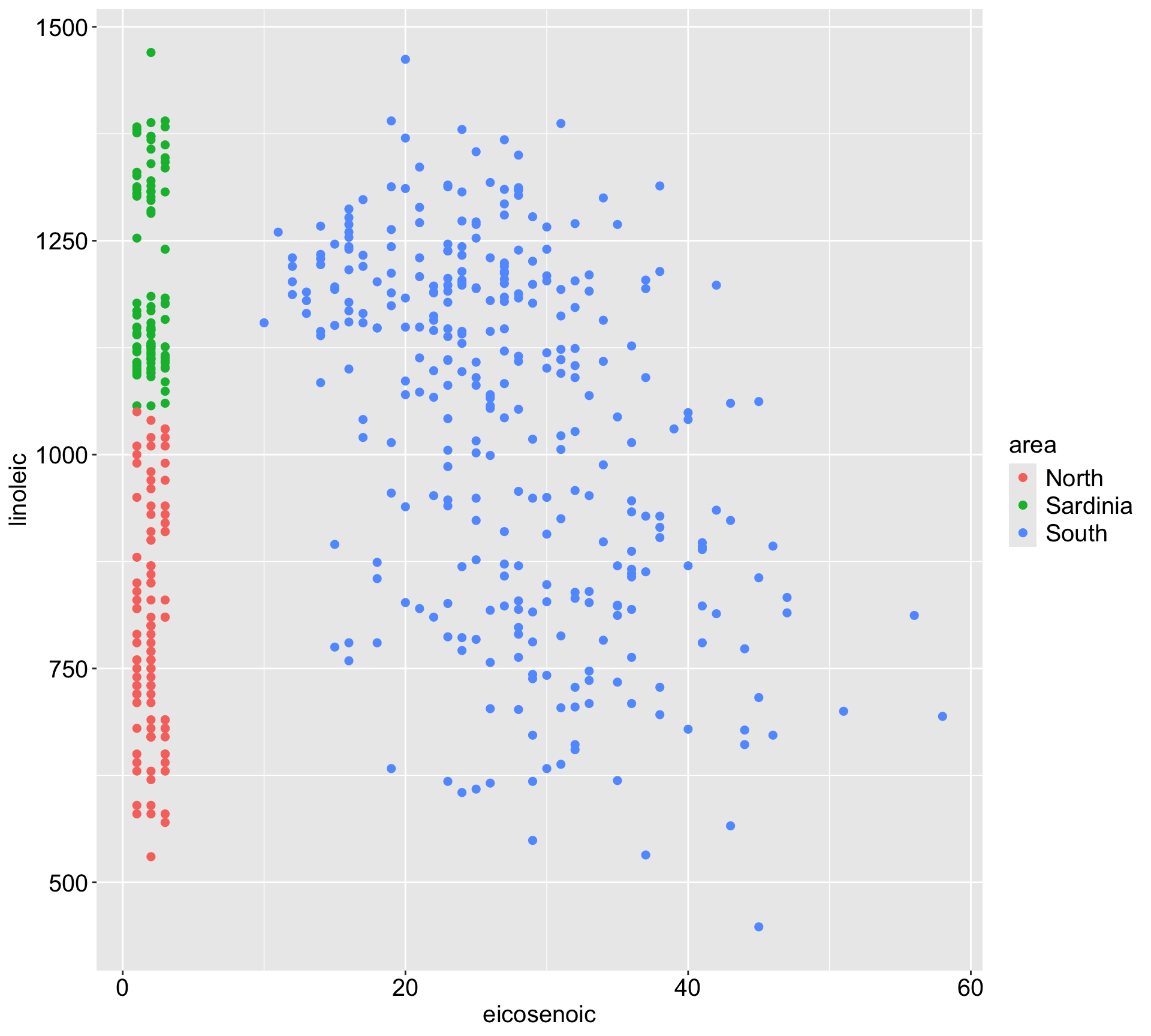
If we would like to predict the area from x1 (eicosenoic) and x2 (linoleic), would you expect linear regression or KNN to perform well?

Decision rules

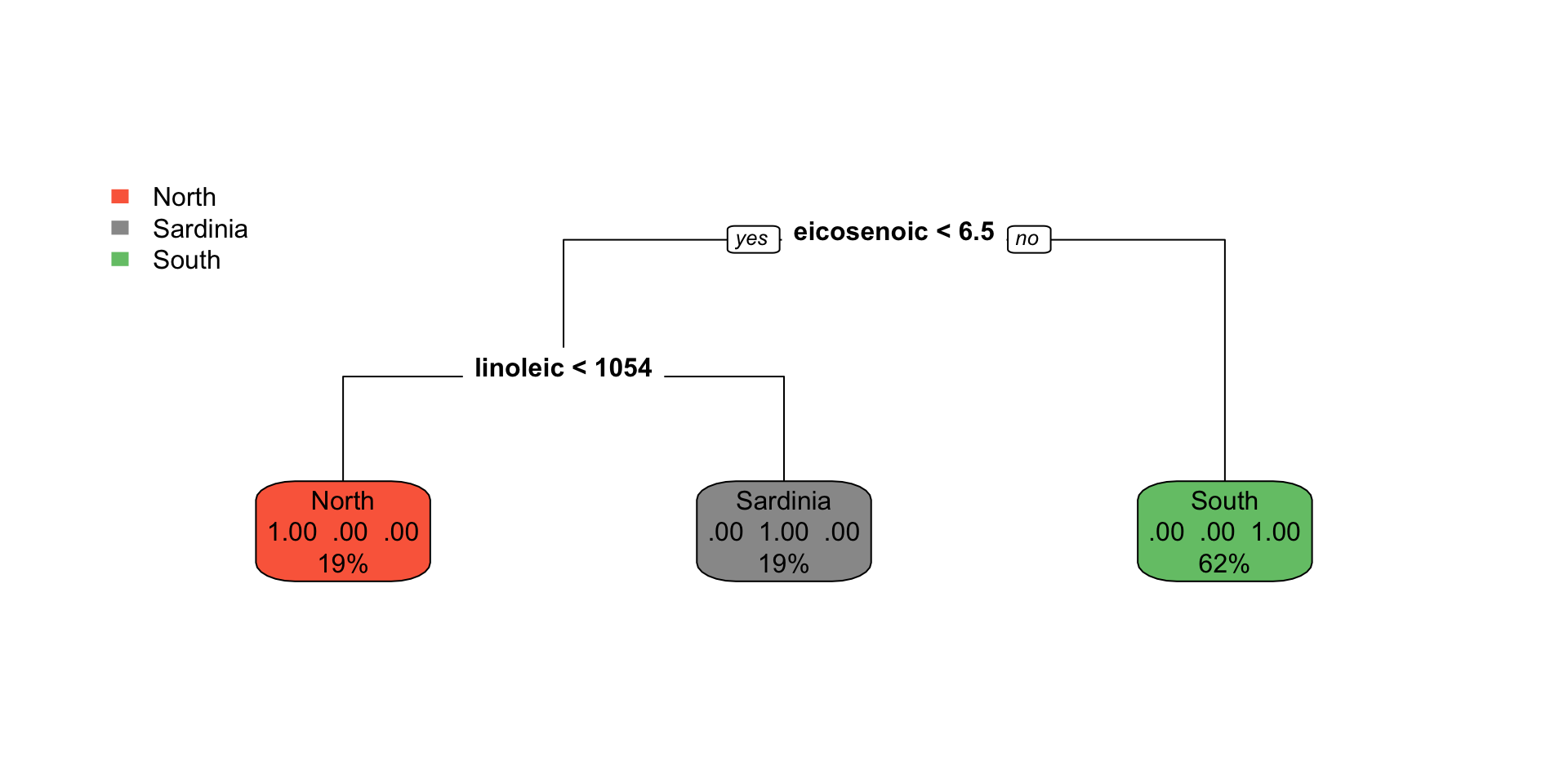
Regression tree

  • Divide/partition the predictor space \(X_1, \ldots, X_p\) into \(J\) regions \(R_1, \ldots, R_J\).

  • For every observation that falls within region \(R_j\), we make the same prediction \(\bar{y}_{R_j}\), which is the mean of the response values for the training observations in \(R_j\).

  • For regression, the overall goal is typically to minimize the residual sum of squares:\[ RSS = \sum_{j=1}^{J} \sum_{i \in R_j} (y_i - \bar{y}_{R_j})^2\]

Regression tree with tidymodels

Step 1/2/3: specify the model/ recipe/ workflow:

dt_reg_spec <- decision_tree(mode = "regression", engine = "rpart", min_n = 150)
dt_recipe <- recipe(body_mass ~ bill_len + bill_dep, data = datasets::penguins) |> 
  step_naomit()
dt_wf <- workflow() |> add_model(dt_reg_spec) |> add_recipe(dt_recipe)

Step 4: fit the tree:

set.seed(1)
dt_cls_fit <- dt_wf |> fit(data = datasets::penguins)

Step 5/6: predict/ calculate the prediction accuracy metrics:

dt_cls_fit |> augment(datasets::penguins) |> metrics(truth = body_mass, estimate = .pred)
# A tibble: 3 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard     560.   
2 rsq     standard       0.511
3 mae     standard     416.

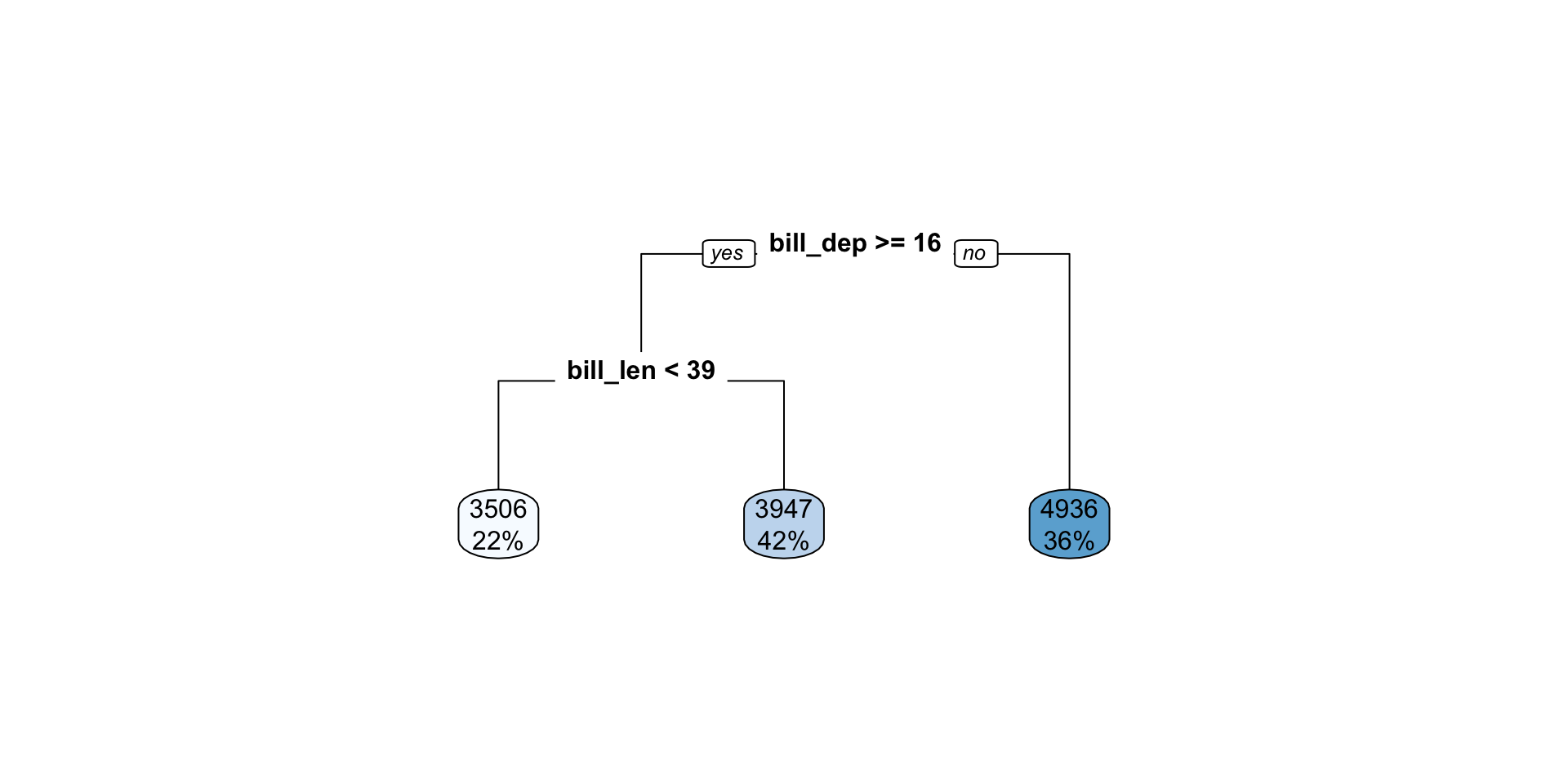
Regression tree with tidymodels

dt_cls_fit |> extract_fit_engine()
n=342 (2 observations deleted due to missingness)

node), split, n, deviance, yval
      * denotes terminal node

1) root 342 219307700 4201.754  
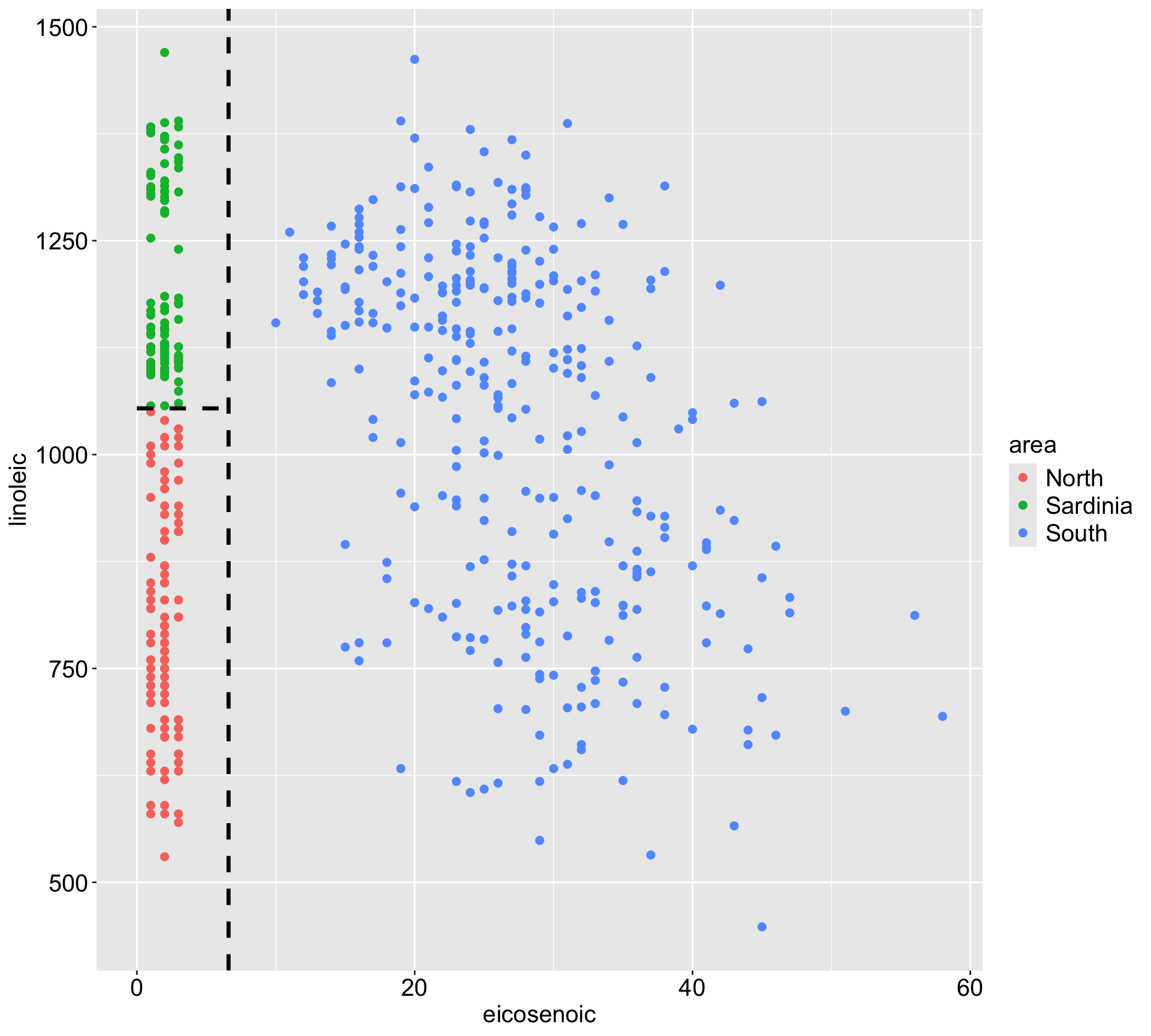
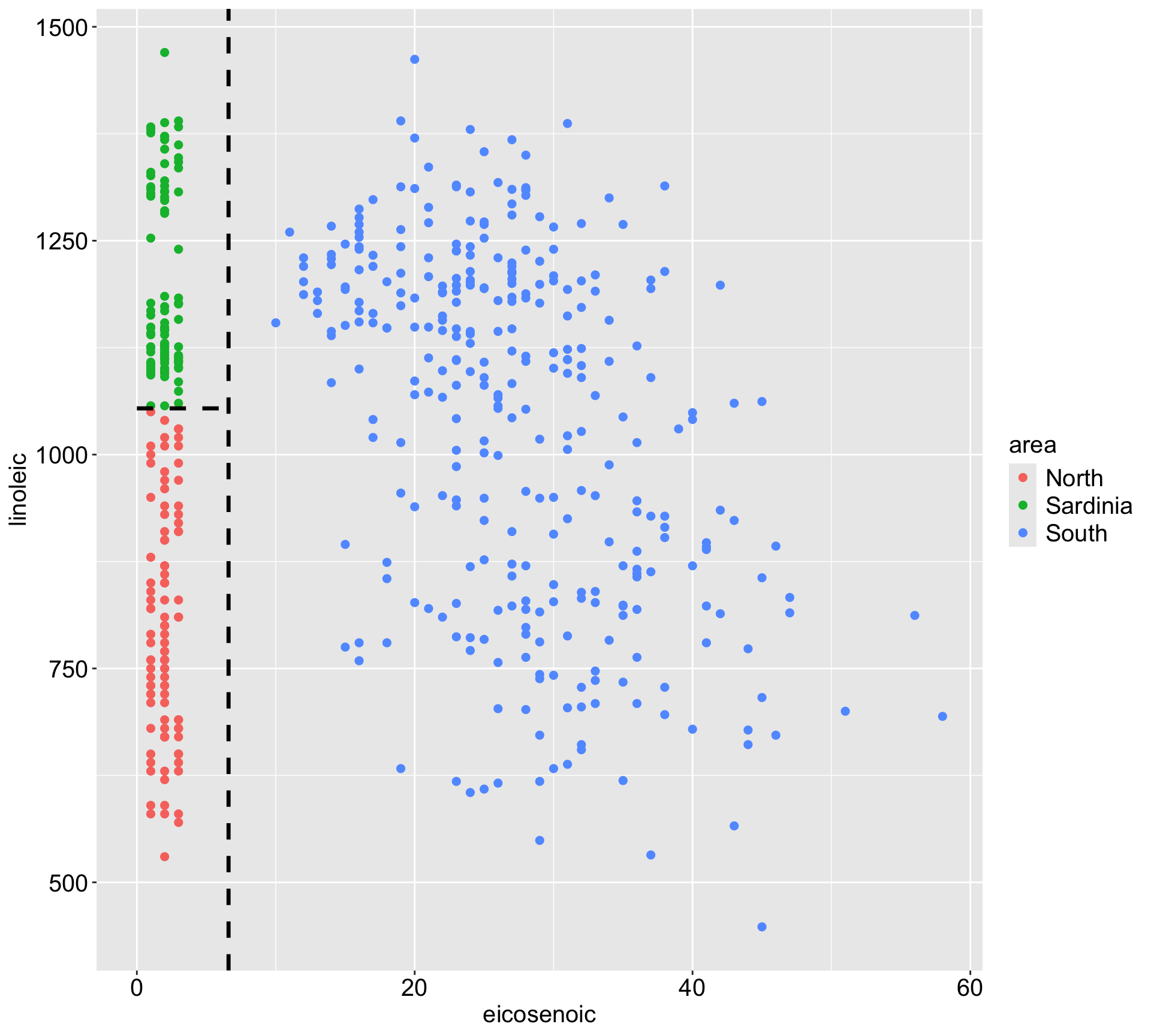
  2) bill_dep>=16.45 220  65255400 3794.318  
    4) bill_len< 39.05 76   9524836 3505.921 *
    5) bill_len>=39.05 144  46073260 3946.528 *
  3) bill_dep< 16.45 122  51673930 4936.475 *
library(rpart.plot)
dt_cls_fit |> 
  extract_fit_engine() |> 
  rpart.plot::rpart.plot(type = 0)

Visualize the space

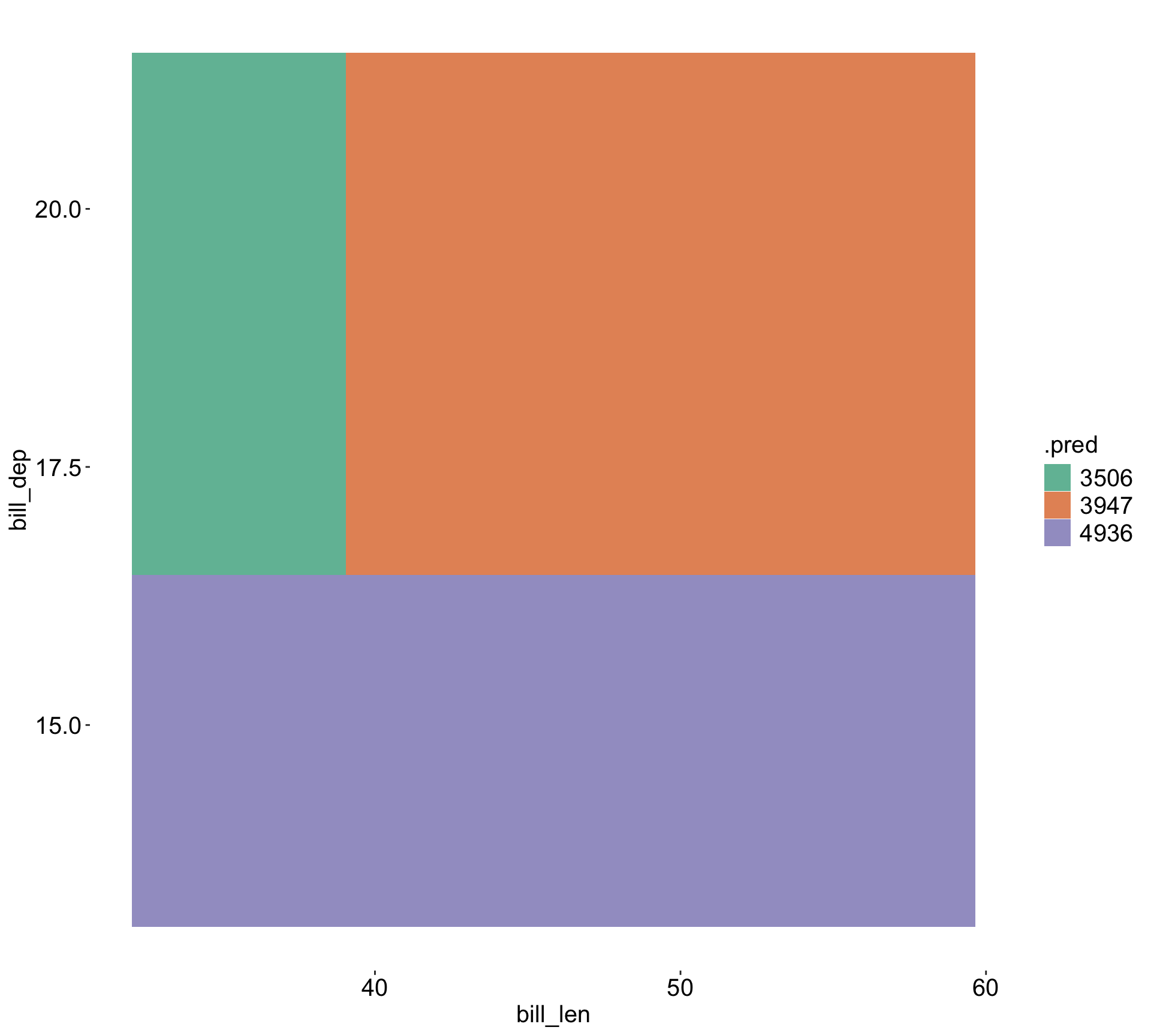
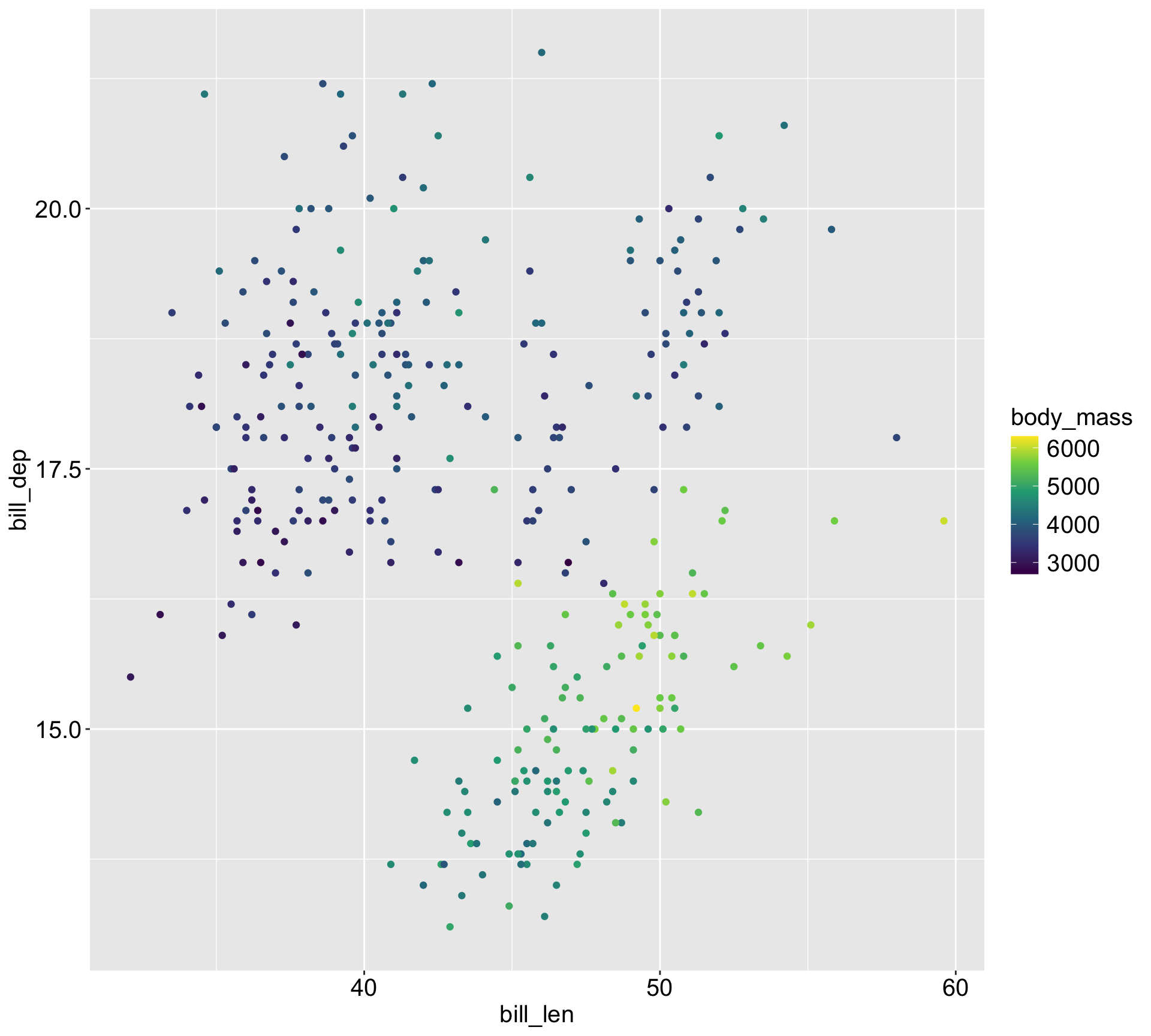
Species Adelie Chinstrap Gentoo
Average body mass 3701 3733 5076

Classification tree

  • Classification trees use the same splits, but minimize impurity (not RSS).
  • Classification of an observation is taken as the majority class in a region
  • Goal is to increase the “purity” of each region so that most regions are dominated by a single class

Classification tree

Let \(p_{mk}\) be the proportion of training observations in region \(R_m\) that are from class \(k\). For region \(R_m\),

The Gini index: \(G(R_m) = \sum_{k=1}^{K} p_{mk}(1 - p_{mk})\). lower, purer.

The Entropy: \(H(R_m) = - \sum_{k=1}^{K} p_{mk} \log(p_{mk})\). lower, purer.

Example:

After a certain split, we have 10 observations in region \(R_m\), with

class 1 class 2 class3
4 3 3

Then, we may calculate:

  • Gini index: \(G(R_m) = 0.4 *(1- 0.4) + 0.3 * (1-0.3) + 0.3 * (1-0.3) = 0.66\)
  • Entropy: \(H(R_m) = - (0.4 \log 0.4 + 0.3 \log 0.3 + 0.3 \log 0.3) = 1.09\)

Here we predict class 1 since it is the majority vote.

Classification tree

The next cut may be dividing these 10 observations into two regions:

  • \(R_{m1}\) with 6 observations (4 from class 1, 2 from class 2) and
  • \(R_{m2}\) with 4 observations (1 from class 2, 3 from class 3).

Then we would predict class 1 for \(R_{m1}\) and class 3 for \(R_{m2}\).

  • Gini index:

    • \(G(R_{m1}) = 4/6 * (1-4/6) + 2/6 * (1- 2/6) = 0.44\),
    • \(G(R_{m2}) = 1/4 * (1 - 1/4) + 3/4 * (1-3/4) = 0.375\)

  • Entropy:

    • \(H(R_{m1}) = -(4/6 * log(4/6) + (2/6) *log(2/6)) = 0.64\),
    • \(H(R_{m2}) = - (1/4 * log(1/4) + 3/4 * log(3/4) = 0.56\)

Why does purity matter?

Example: Classification tree with tidymodels

Step 1/2/3: Setup the recipe/ model/ workflow:

library(tidymodels)
dt_cls_spec <- decision_tree(mode = "classification", engine = "rpart", min_n = 15) 
dt_recipe <- recipe(sex ~ bill_len + bill_dep, data = datasets::penguins) |> 
  step_naomit()
dt_wf <- workflow() |> add_model(dt_cls_spec) |> add_recipe(dt_recipe)

Step 4: Fit

set.seed(1)
dt_cls_fit <- dt_cls_spec |> fit(sex ~ bill_len + bill_dep, data = datasets::penguins)

Step 5: Predict/ Calculate classification metric

pred_df <- dt_cls_fit |> augment(datasets::penguins) 
pred_df |> 
  conf_mat(truth = sex, estimate = .pred_class)
          Truth
Prediction female male
    female    138   19
    male       27  149
pred_df |> 
  accuracy(truth = sex, estimate = .pred_class)
# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy binary         0.862

Classification tree with tidymodels

library(rpart.plot)
dt_cls_fit |> 
  extract_fit_engine() |> 
  rpart.plot::rpart.plot(type = 0)

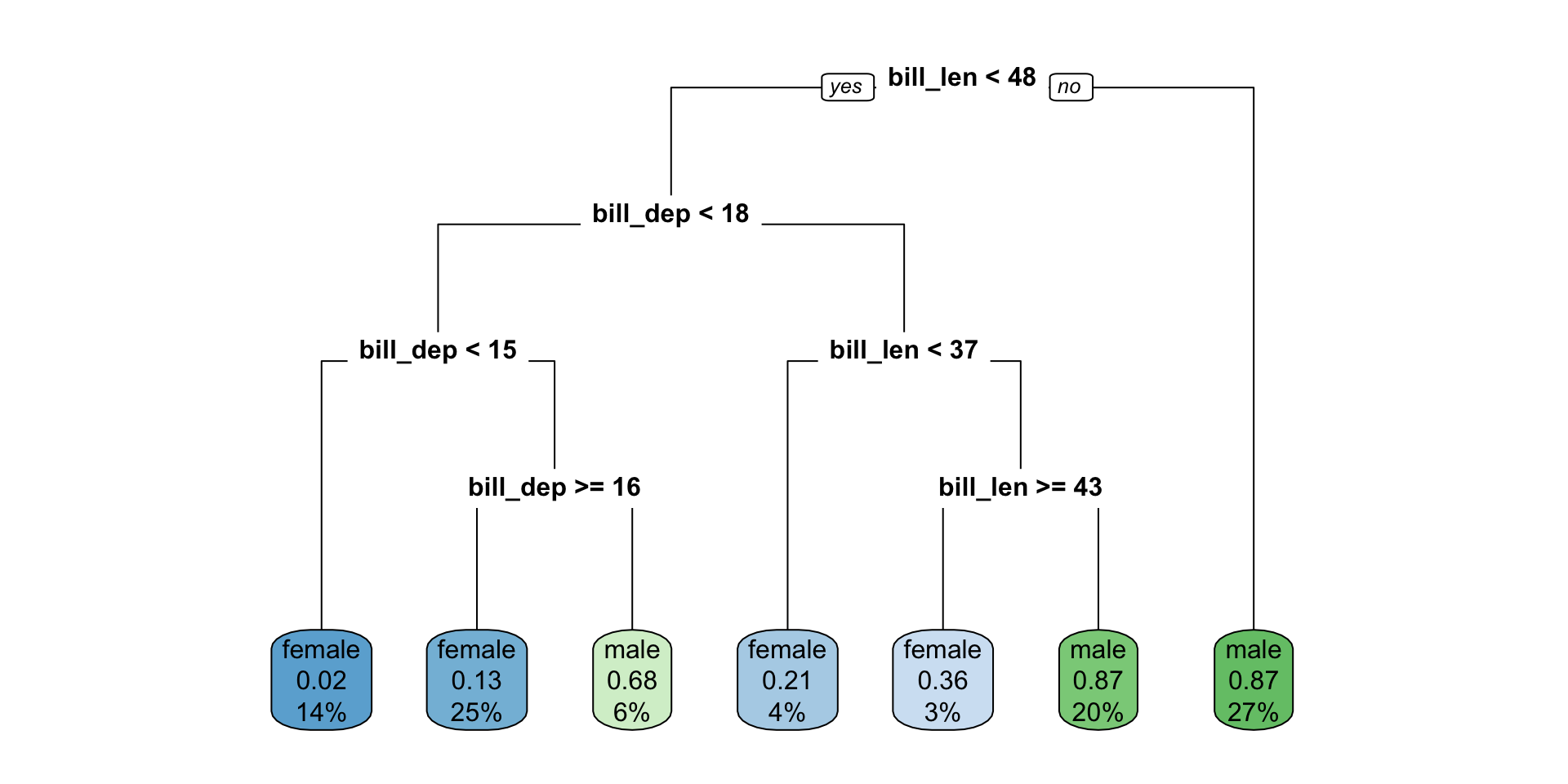
Visualize the space

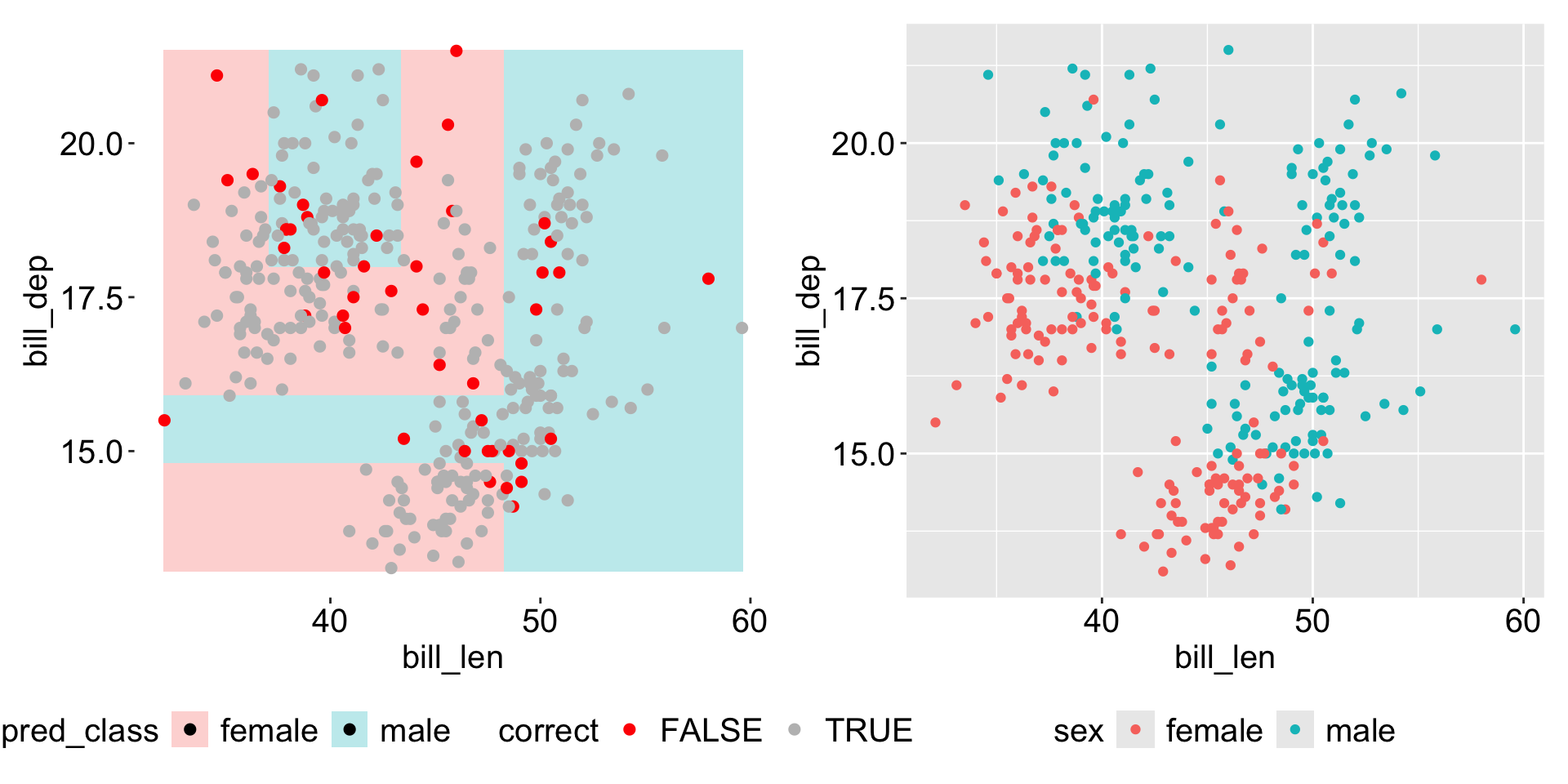
More details on the tree parameters

  • By default, the Gini index is used for splitting the tree, to change to entropy, use
 decision_tree(mode = "classification") |> 
  set_engine("rpart", parms = list(split = "information"))

  • Trees have a few hyper-parameters that you may want to tune:

    • min_n: minimum number of data points in a node required for the node to be split further
    • cost_complexity: complexity parameter that penalizes large trees
    • tree_depth: maximum depth of the tree